结构设计中我们总是在各种矛盾的因素之间寻求最优方案，结构、功能、美学需求一个都不能少，但是应该优先考虑哪一项呢？当然不同的项目有不同的答案，但目的都是要找到一个综合各项指标的最优的结构方案。

在寻找最优结构方案的过程中，有两个因素对结构性会有重大影响：内力分布和几何形状。

在找形中，首先必须明确如何的几何形状能够在结构中实现最优的力传导；得到几何形状后的完善阶段，工作的焦点又会转移到形体和构造方面；然而这两个阶段之间的界限经常是模糊的。

通过找形实现最优的力传导

设计一个高效的结构，关键是要优化结构材料的用量。通过优化结构受力则可以提高材料的利用率，这个过程主要遵循以下两个简单的指导原则：

避免弯矩

力在构建横截面上是均匀分布的，这样材料才可能达到100%的利用率。

拉力比压力传递荷载更高效

原因就是受压杆件会有失稳的可能。我们可以想象一下一把尺子在受压时的状态，便很容易理解这种现象。

谨记上述原则是设计高效的结构体系的前提，如下图示例，轻型索网结构体系和膜结构体系同样遵循了上述原则。

▲ 1972年德国慕尼黑奥林匹克体育场屋盖

形态动人同时又高效的结构体系也是可能实现的。悬索桥便是其中一类案例。

▲ 德国波鸿人行桥

▲德国盖尔森基兴人行桥

虽然拉力比压力传递荷载更高效，但很少有项目是仅靠拉力体系就能实现的，即使是最高效的结构如索网和膜结构体系，受压杆件也必不可少。所以，对于大多数的项目，最佳的结构方案是将轴向受压和受拉杆件进行巧妙地组合。

研发的一种计算工具能够结合受拉杆件和受压杆件以及弯矩，有效地分析不同设计参数下的不同的设计方案，同时结合创新的设计方式，有助于设计出独特的最优方案，这个优化的过程可以从方案阶段一直延伸到初步设计阶段甚至施工图阶段。

位于德国勒沃库森的BayArena的体育场是一座典型的采用环索屋盖结构体系的体育场，在它的外边缘上采用了2个压环，在中间采用1个拉环，压环与拉环之间通过径向索连接。

位于苏州的苏州奥林匹克体育中心包括一座体育场、一座游泳馆和一座体育馆，其马鞍形的屋盖采用了单层索网结构。

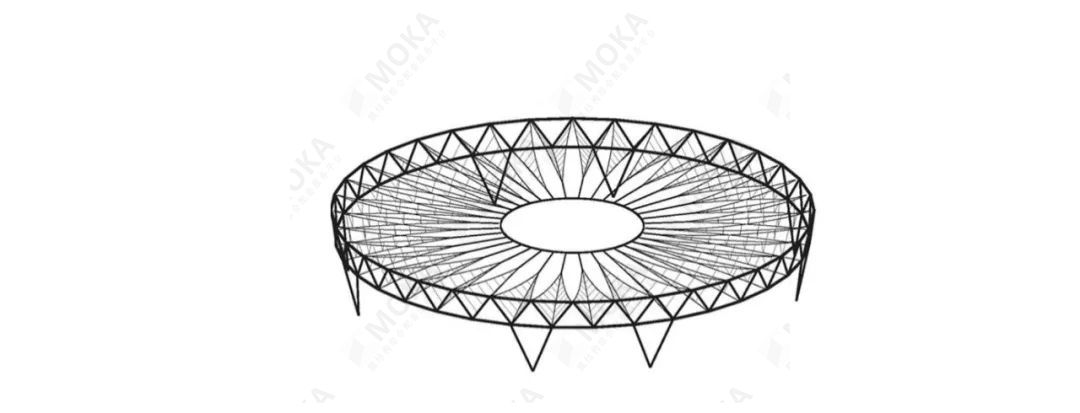
▲ 德国勒沃库森拜耳球场：经过找形分析，屋盖结构的荷载仅传递至8根V柱

▲ 苏州奥林匹克体育中心

找形在其它方面的功用

对几何形状进行优化除了有助于优化结构受力之外，在其它方面例如在减小加工难度方面，也有所帮助。    现代科技发展水平下，找形的目的已不仅仅是为了勾勒和组织空间形状。在考虑高效性和美观性的同时，找形也会对结构、形状和施工相关的参数进行优化。    通过面板划分，可以使几何形状相同的面呈现不同的外观表现形式，合理的面板划分可以加强面的三维效果，该优化过程同时也会考虑模块组件的运输要求。通过采用创新的优化方法，任何面都可以被划分为优雅、规则的形状，同时在找形的过程中也会考虑杆件加工和细节上的具体的要求。

“自内而外”和“自外而内”是两个不同的找形过程。

译者注：此处中文翻译为自内而外及自外而内更贴进与英文原意。自内而外的意思是遵循几何基本原理而产生相应的外观，自外而内的意思是从已知的设计边界条件甚至外观来定义形式。

在“自内而外”的找形过程中，自由曲面整体形状可以参数化确定线段构成。提出的利用 “轨迹线成面” 几何原则可以形成由规则的构件组成的自由曲面；例如具有相等杆件长度的平面四边形及无任何翘曲的玻璃。“自内而外”流程的第一个应用案例是位于柏林动物园河马之家的屋盖。自此以后，该原则被成功运用到多个项目中。然而在这种方法中，几何形状会受到所选择的结构构件所限制。

▲ 柏林动物园河马之家的屋盖

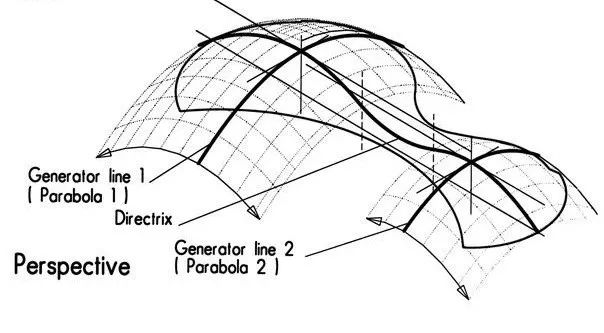
▲ 屋盖结构的设计原理

与该方法不同的是，“自外而内”的方法是一种采用已经基本确定好外观形状而再设计或找形的过程。将确定的外观与单个的网格进行重叠，并根据不同的设计要素如建筑外观、生产难度、模块化等对这些网格进行优化。利用相应的几何算法去优化这样的异形网格结构。由于这样的找形方式自由度和灵活性更大，尤其是可以大幅度地优化已经由建筑师或业主已经确定的几何形体，对此方法尤其在建筑外表皮上的运用进行了更深入的研究和应用。

整体优化过程中也会考虑局部结构的要求，例如杆件的均匀度、内角的标准化或期望的杆件长度，并将它们转化为比例良好的空间网格，同时不会偏离既定的几何形状。

对于找形所产生的优化几何形状，再进行结构分析和优化。

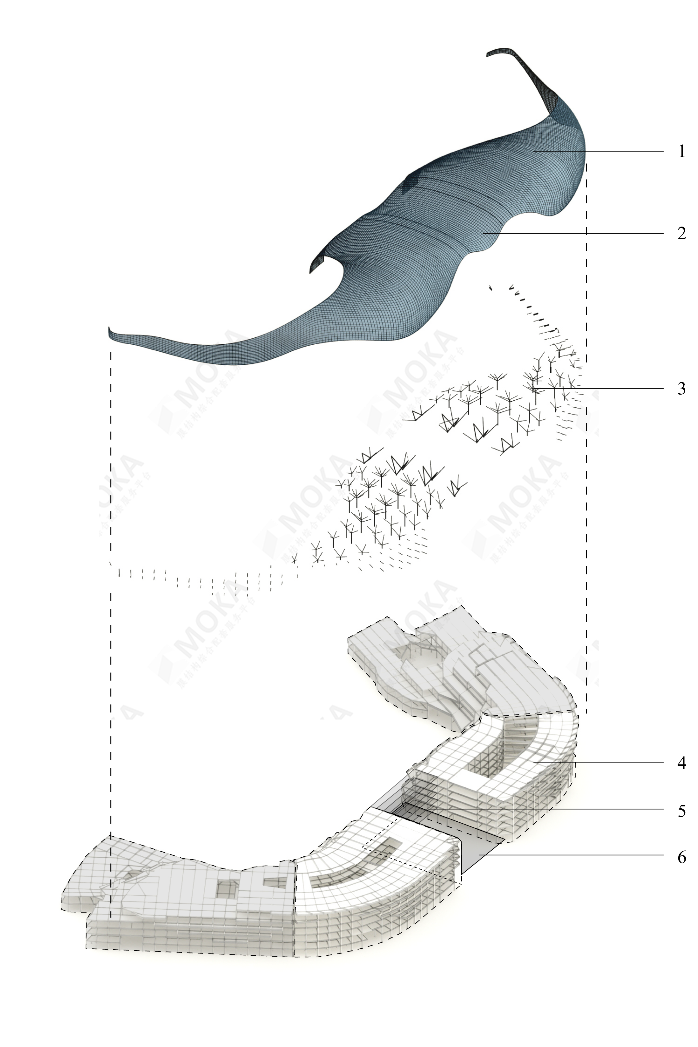
苏州中心大跨度屋盖“未来之翼”采用了这种“自外而内”的方法。

▲ 苏州中心大型屋盖

受业主委托进行该屋盖的结构设计。该屋盖造型的灵感来自凤凰的翅膀。为了减少屋盖在平面内的内力，屋盖发展过程中摒弃了面内刚度更大的三角网格形式，而选择了更具弹性的四边形网格形式。进一步的，便有了在自由形态曲面上进行四边形网格划分的研究发展。

本项目设计过程中的一个核心是完成屋面的分级网格划分，这个过程中屋面的几何形状和结构性能均得到了数学优化。

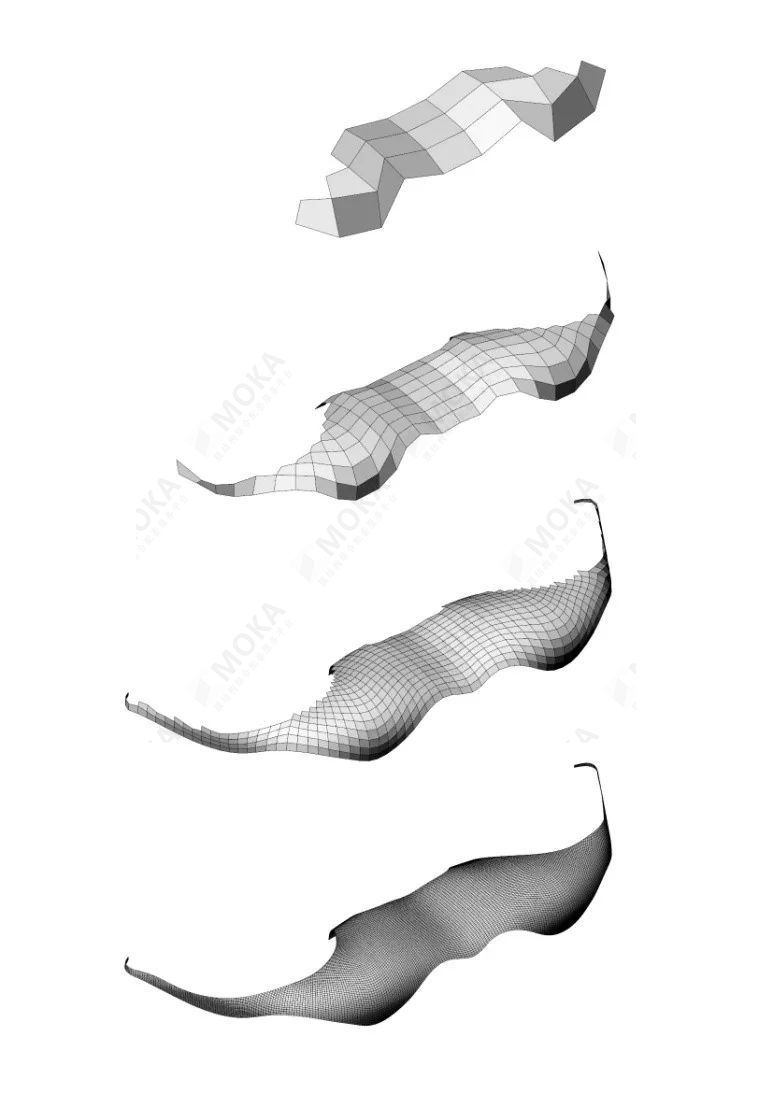
▲ 图：网格的迭代优化过程：由一开始的的基础网格（顶部图）开始，网格细分逐步进行

然而，这样的形式在实现过程中也存在着一些严格的限制因素。网格划分时需要考虑杆件长度的规律性，面的翘曲以及杆件夹角的协调。采用细分曲面法获得了最有效的基础网格框架。通过在Grasshopper中执行Catmull-Clark网格细分法则，设计过程中的一些具体问题得到了解决，例如处理边界条件，亦或只是简单地允许在网格边界采用三角形网格。

在基础网格的基础上，对整体进行了细化的，彻底的网格划分。根据对网格划分结果的定量分析，可以评估是否需要进行进一步的优化。通过这样的方式，可以高效的实现网格划分并将其呈现给建筑师以供讨论。

这样的方法允许单独提出某些屋盖区域，进行局部的“找形”，然后又将该部分屋盖与相邻区域进行无缝组装。优化的准则会根据优化的区域进行选择，其可以是几何性或是结构性的准则，也可以同时执行。举个例子，在中庭区域，杆件中的弯矩被最小化。当网格细分结果使得局部网格到相邻网格之间的过渡是顺畅，无需人工调整的时候，即可以认为找到了最优的下悬网格。

▲ 图：中庭区域的找形步骤图示。1. 网格的初始形态，2. 网格的节点坐标优化， 3. 优化后杆件的弯矩图。弯矩峰值出现在树形柱与网格的交点位置，其他部分杆件的弯矩可以忽略不计。右图：局部放大的弯矩图

在边缘及过渡区，局部的曲度被减小直到面板翘曲在允许的范围之内或者更小，同时考虑对外部几何形状影响最小，所有最不利工况下的偏转最小。

此外，也对网格单元根据几何形状相似度进行了归类以便后期标准化玻璃面板的使用，减少非标准尺寸网格单元的数量。

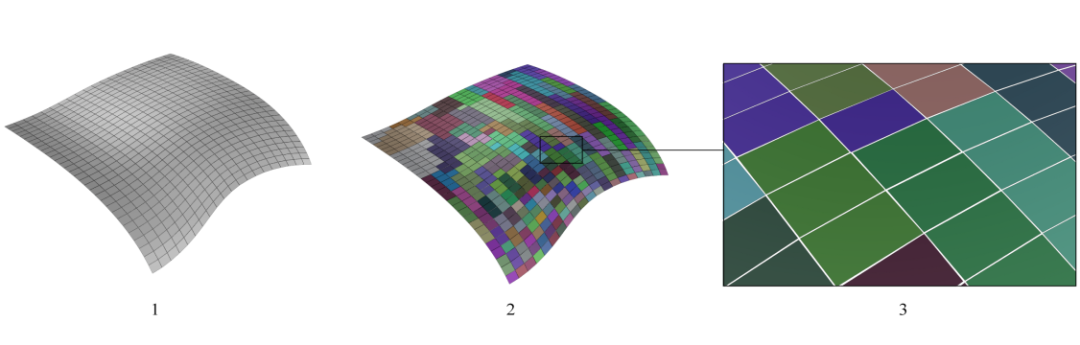
▲ 图：玻璃面板归类。1.  中央下悬网架的一部分， 2. 归类。同色的玻璃面板几何尺寸相同， 3. 由结构分析决定的玻璃面板间缝隙一般控制在3-6cm

总结

项目设计过程中，我们总是力求赏心悦目的外形，同时关注高效的结构，研究对受力的优化和对加工难度的优化。找形可以解决几何形状与结构受力这两项要素之间的对接问题，无论对于建筑师还是工程师而言，都是一项非常有价值的设计过程。